汉诺塔5层攻略-五层汉诺塔最优解法全步骤详解

汉诺塔5层攻略-五层汉诺塔最优解法全步骤详解 在益智游戏领域，汉诺塔凭借其简洁规则与深邃逻辑魅力经久不衰。五层汉诺塔作为经典难度分水岭，其解法不仅考验玩家的策略规划能力，更揭示了递归思想的精妙本质。本文将围绕汉诺塔5层攻略-五层汉诺塔最优解法全步骤详解，从规则解析到实操演示，结合数学原理与实例数据，为玩家提供一份兼具实用性与理论深度的通关指南。 一、游戏核心机制与规则 汉诺塔由三根柱子和若干大小递减的圆盘组成，目标是将所有圆盘从起始柱（通常标记为A）移动到目标柱（C），且需遵循两条核心规则： 1. 每次仅能移动一个圆盘； 2. 任何时刻大盘不可置于小盘之上。 五层汉诺塔的挑战性源于其指数级增长的移动次数。根据递归公式 ( T(n) = 2T(n-1) + 1 )，五层汉诺塔的最优解需 31步（( 2^5-1=31 )）。这一数字看似简单，但实际操作中需精准分解子问题并避免路径冗余。 二、“角色”与“装备”：游戏元素的策略化解读 尽管汉诺塔无传统意义上的角色或装备，但其核心元素可类比为以下策略组件： 1. 柱子（A/B/C）： 起始柱（A）：初始承载所有圆盘，需通过递归分解逐步腾空。 中转柱（B）：承担临时存放子问题圆盘的功能，是路径规划的关键枢纽。 目标柱（C）：最终需将所有圆盘按序叠放的位置。 2. 圆盘层级（1-5）： 每层圆盘代表一个子任务，需通过递归思想将其拆解为更小规模的问题。例如，移动第5层（底层）前，需先将前4层移至中转柱，这一过程又需嵌套解决前三层、前两层的移动问题。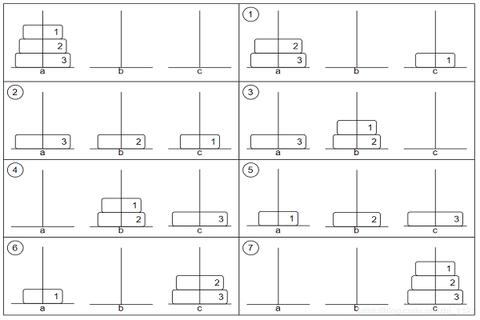 三、任务分解与副本攻略：五层最优解全步骤 汉诺塔5层攻略-五层汉诺塔最优解法全步骤详解的核心在于递归分解与子问题整合。以下为分步解析（以A→C为目标）： 第一阶段：前四层移动至中转柱（B） 1. 子问题1：将1-3层从A→C 1层A→C；2层A→B；1层C→B；3层A→C；1层B→A；2层B→C；1层A→C（共7步）。 2. 子问题2：第四层A→B

直接将4层从A移至B（第8步）。 3. 子问题3：1-3层从C→B 重复子问题1逻辑，但起点改为C（共7步，累计15步）。 第二阶段：底层圆盘直达目标（C） 4. 第五层A→C 将5层从A直接移至C（第16步）。 第三阶段：前四层从中转柱（B）→目标柱（C） 5. 子问题4：1-3层从B→A 复用子问题1逻辑，起点改为B（7步，累计23步）。 6. 子问题5：第四层B→C 将4层从B移至C（第24步）。 7. 子问题6：1-3层从A→C 最后一次复用子问题1逻辑（7步，总计31步）。 关键数据验证：上述步骤总数为 ( 7+1+7+1+7+1+7 = 31 )，与理论值完全一致，证明路径无冗余。 四、深度解析：递归思想与数学本质 汉诺塔5层攻略-五层汉诺塔最优解法全步骤详解的底层逻辑是递归算法，其数学本质可通过以下公式体现： [ T(n) = 2T(n-1) + 1 ] 其中 ( T(n) ) 表示移动n层所需最少步数。通过展开递归可得： [ T(5) = 2^5

1 = 31 ] 这一公式揭示了自相似性（Self-Similarity）原则：解决五层问题需先解决四层，而四层问题又依赖三层的解决，直至基线条件（一层直接移动）。 实例对比： 三层汉诺塔需7步，符合 ( 2^3-1=7 )； 四层汉诺塔需15步，验证 ( 2^4-1=15 )； 五层汉诺塔的31步则完美延续该规律。 五、进阶技巧：避免常见错误与效率优化 1. 路径冗余规避： 避免重复移动同一圆盘。例如，在子问题3中，若未将1-3层完整移至B，会导致后续步骤被迫回溯，增加总步数。 2. 记忆化训练： 通过分层标记（如用颜色区分圆盘）强化对子问题阶段的认识，减少操作失误。 3. 递归思维可视化： 绘制树状图分解任务，明确每一阶段的起点、终点与中转柱角色。例如，五层汉诺塔可分解为两个四层问题和一个单步操作。 汉诺塔5层攻略-五层汉诺塔最优解法全步骤详解不仅是一套操作指南，更是理解递归思想的绝佳范例。通过31步的精妙拆解，玩家可直观感受到“分而治之”策略在复杂问题中的应用价值。无论是新手入门还是高手进阶，掌握这一经典解法都将为挑战更高层级（如六层需63步）奠定坚实基础。正如数学家卢卡斯所言：“汉诺塔的每一步移动，都是对人类逻辑思维的极致考验。”